向中心の円形軌道（ノーズインサークル）の数学

 

以下、数式など綺麗なもので見たい方は、次のpdfをダウンロードしてご覧ください。

向中心円軌道（pdf）

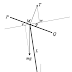
ドローンの向きを一つの方向に固定しながら、ドローンを円形軌道に飛行させようとする場合は、その速度のコントロールは次のようになる。

座標を水平方向に$x$をとって、垂直方向にyをとると、A点を基準にして、機体がB点にあるとし、円の半径を$r$、角速度を$w$、時間を$t$とすると、

$$x = r\sin(wt)$$

$$y = r(1-\cos(wt))$$

であり、これを時間で微分したものが必要な速度となるから、速度をそれぞれ$v_{x}, v_{y}$とすると、

$$v_{x} = rw\cos(wt)$$

$$v_{y} = rw\sin(wt)$$

となる。

ドローンの向きが一定方向に維持されている限り、このような制御でドローンの軌道は円形になる。

しかし、ドローンの向きが常に縁の中心に向くということは、期待そのものが回転しているということである。これは、月が常に地球に同じ面を向けている状況と同じである。 

この場合、上記の方法ではうまくいかない。機体の回転のたびに、座標そのものが回転するからである。ドローンには、機体の座標だけではなく、グラウンド座標というものがあり、その場合は、常に向きが北を基準にするので、違った状況になることが考えられるが、ここではあくまで機体の方向に座標が維持されているとしよう。

このとき、円形軌道となるためには、上記の速度が必要なのだが、機体の速度を上記の速度が実現できるようなものにすれば良い。

回転した状況における、機体を基準とした座標の速度を$u_{x}, u_{y}$としよう。

このとき、速度の分解方向から、

$$u_{x}\cos(wt) - u_{y}\sin(wt) = v_{x} (= rw\cos(wt))$$

$$u_{x}sin(wt) - u_{y}sin(wt) = v_{y} (= rw\sin(wt))$$

という式が成立する。

これを解くと、次のような実に簡単な式になる。

$$u_{x} = rw$$

$$u_{y} = 0$$

つまり、機体を月の自転のように、一周当たり角速度wで回転させておけば、上記の式で機体の速度を維持することによって、常に中心向きにカメラを向けるドローンの制御ができるのだ。あまりにも簡単になるので、信じられなかったが、実際ドローンにこの制御を組み込むと、確かに意図する円形軌道を描いたのである。とても驚いた。