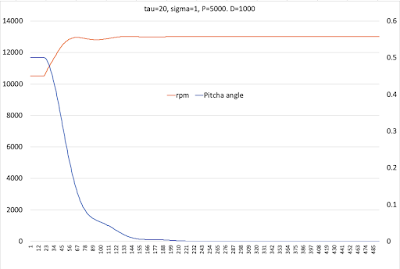
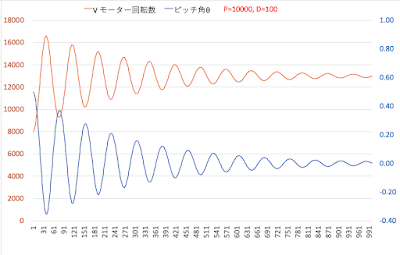
これまでの記述については、以下のページを参考にしてください。
PID制御によるドローンの揺れに関する数値シミュレーション(1):理論編
PID制御によるドローンの揺れに関する数値シミュレーション(2):シミュレーションモデル
モデルについての基本的なコンセプトはこれまでの議論を踏襲する。これまでは、PID制御と言ってもP制御だけを組み込んだモデルを扱ってきた。確かに、P制御は基本的なものだが、結果として、機体の揺れは、収束には向かうものの時間がかかったり揺れの大きさでドローンを安定させるためには不十分なものだった。
そこで、ここではさらにD制御もモデルの中に組み込んでその効果を確認する。
すなわち、
$$V=V_{0}-P\theta-D\frac{d\theta}{dt}$$
とする。$V$はモーター回転数(rpm)で、$V_{0}$は、ホバリングを可能にする定常回転数である。$\theta$はピッチ角であり、$t$は時間である。$P$は制御係数でピッチ角に比例して、その揺れを抑える方向に回転数を調整する。$D$は、揺れの急激な変化に反応する微分項である。
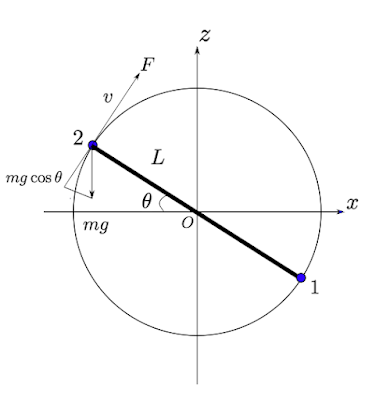
モーターの推力$F$は、次のようになる(パラメータの意味および式の解説はこれまでの記事を参考にしていただきたい)。
$$\begin{eqnarray*}F & = & \delta V^{2} \\& = & \delta \left(V_{0}-P\theta-D\frac{d\theta}{dt}\right)^{2} \\& = & \delta \left(V_{0}^{2}+P^{2}\theta^{2}+D^{2}\left(\frac{d\theta}{dt}\right)^{2}-2V_{0}P\theta+2P\theta D\frac{d\theta}{dt}-2V_{0}D\frac{d\theta}{dt}\right)\end{eqnarray*}$$
これを運動方程式
$$mL\frac{d^{2}\theta}{dt^{2}}=F-mg\cos \theta$$
に代入し変形すると、
$$\begin{eqnarray*}\frac{d^{2}\theta}{dt^{2}}&=&\frac{\delta}{mL} \left(V_{0}^{2}+P^{2}\theta^{2}+D^{2}\left(\frac{d\theta}{dt}\right)^{2}-2V_{0}P\theta+2P\theta D\frac{d\theta}{dt}-2V_{0}D\frac{d\theta}{dt}\right)\\& &-\frac{g}{L}\cos \theta\end{eqnarray*}$$
となる。これまでと同様に、これは特殊な二階非線形常微分方程式で帯域的な解を求めることはできるのかもしれないが、一般に困難なものとなる。ここでの目的は、数値的解が目的なので、一般解にこだわる理由もない。
4次のルンゲ・クッタ法で解くためのモデルを示そう。
まず、この二階の常微分方程式を一階の連立常微分方程式に変換する。角速度を$\omega$とすると、
$$\begin{eqnarray*}\frac{d\theta}{dt}&=&\omega\\\frac{d\omega}{dt}&=&\frac{\delta}{mL} \left(V_{0}^{2}+P^{2}\theta^{2}+D^{2}\left(\frac{d\theta}{dt}\right)^{2}-2V_{0}P\theta+2P\theta D\frac{d\theta}{dt}-2V_{0}D\frac{d\theta}{dt}\right)\\& &-\frac{g}{L}\cos \theta\end{eqnarray*}$$
簡単化のため、この第2式を次のように表そう。
$$\frac{d\omega}{dt}=a+b\theta+c\theta^{2}+d\omega+e\theta\omega+j\omega^{2}+s\cos\theta$$
各係数は次のようなものである。
$$\begin{eqnarray*}a & = & \frac{\delta V_{0}^{2}}{mL}\\b & = & -\frac{2\delta V_{0}P}{mL} \\c & = & \frac{\delta P^{2}}{mL}\\d & = & -\frac{2D\delta V_{0}}{mL}\\e & = & \frac{2DP\delta}{mL}\\j & = & \frac{\delta D^{2}}{mL}\\s & = & -\frac{g}{L}\end{eqnarray*}$$
モデルの記述をわかりやすくするために、ここで次のような関数を定義する。
$$\begin{eqnarray*}f(\omega_{n},\theta_{n},k^{\omega},k^{\theta})&=&a+b(\theta+k^{\theta})+c(\theta^{2}+k^{\theta})+d(\omega+k^{\omega})\\& &+e(\theta+k^{\theta})(\omega+k^{\omega})+j(\omega+k^{\omega})^{2}\\& &+s\cos(\theta+k^{\theta}))\end{eqnarray*}$$
これは、EXCELで計算するときに、VBAで定義しても使う。これを使うと、微分方程式を解くための漸化式は次のように定式化できる。$n = 0, 1, 2 \cdots$は、繰り返される時間、ステップを表している。
$$\begin{eqnarray*}k_{1}^{\theta}&=&h\omega_{n}\\k_{1}^{\omega}&=&hf(\omega_{n},\theta_{n},0,0)\\k_{2}^{\theta}&=&h(\omega_{n}+\frac{k_{1}^{\omega}}{2})\\k_{2}^{\omega}&=&hf(\omega_{n},\theta_{n},\frac{k_{1}^{\omega}}{2},\frac{k_{1}^{\theta}}{2})\\k_{3}^{\theta}&=&h(\omega_{n}+\frac{k_{2}^{\omega}}{2})\\k_{3}^{\omega}&=&hf(\omega_{n},\theta_{n},\frac{k_{2}^{\omega}}{2},\frac{k_{2}^{\theta}}{2})\\k_{4}^{\theta}&=&h(\omega_{n}+k_{3}^{\omega})\\k_{4}^{\omega}&=&f(\omega_{n},\theta_{n},k_{1}^{\omega},k_{1}^{\theta})\\\theta_{n+1}&=&\theta_{n}+\frac{1}{6}(k_{1}^{\theta}+2k_{2}^{\theta}+2k_{3}^{\theta}+k_{4}^{\theta})\\\omega_{n+1}&=&\omega_{n}+\frac{1}{6}(k_{1}^{\omega}+2k_{2}^{\omega}+2k_{3}^{\omega}+k_{4}^{\omega})\end{eqnarray*}$$
初期値、$\theta_{0}$および$\omega_{0}$が与えられると、上から順に代入していけば、$\theta_{1}$および$\omega_{1}$が得られ、これを繰り返すことによって機体角とその加速度の系列を得ることができる。
EXCELによる実際の計算とその結果は次回示します。
このシリーズの記事目次。