PID制御によるドローンの揺れに関する数値シミュレーション（１）：理論編

ドローンにPID制御をかけると、安定化は可能であるが同時に機体の揺れも発生させる。この状況を数値シミュレーションする。ただし、今回は、ESCに与える信号と、モーターの回転数の変化の間に遅れが発生しないことを前提にする。このラグのある場合の状況は次に試みる予定だ。

というよりも、もともとこの分析を始めるきっかけが、自作ドローンの信号とモーター回転数の間にあるラグがPID制御の不安定の原因だと思ったことだ。それを分析したいのだが、まず単純でピュアな状態を分析しなければ話にならないので、最初はその前提で進める。

モデルを示そう。

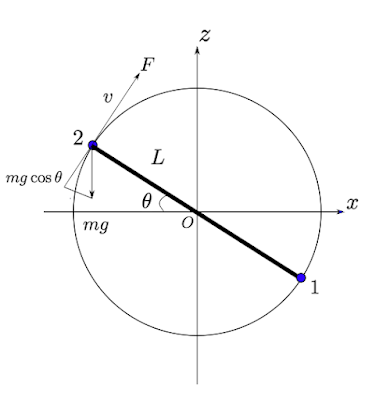
4ローターのドローンを想定しているが、問題の趣旨から、ロールないしはピッチの片方だけ考慮すればよい。上図のように、モーターの腕方向に機体座標が設定されているとする。

ピッチをイメージしよう。先頭のモーター番号を1後方を２とする。zが垂直方向で、xがピッチが現れる水平方向である。

機体が太黒線のように傾いた状態を考える。また、問題はさらに単純化できる。

今、二つのモーターが完全に対称に動くとすると、原点Oが固定されていて、一方のモータの動きだけで回転する状況を想定すればよい。今そのモータを2番のモーターだとしよう。以後、１番のモーターの動きは問題にしない（Oが固定されているので）。

接線方向の運動方程式を立てる。モーターによる推力を$F$とする。重力加速度を$g$、機体のモーターにかかる重さを$m$とする。これは全機体重の1/4と考えてよいかもしれない（深く考えると色々ありそうだが、無視する）。さらに、図のように、機体がピッチが正の方向に$\theta$（ラジアン単位）だけ傾いているとしよう。上向きの接線方向の速度を$v$とすると、運動方程式は次のようになる。

$$\begin{equation} m\frac{dv}{dt}=F-mg\cos \theta \end{equation}\label{eq1}$$

また、角速度を$\omega$とすると、次の式が成立する。

$$\begin{equation}v=L\frac{d\theta}{dt}=L\omega\end{equation}\label{eq2}$$

プロペラの1分あたり回転数を$V$（単位rpm）とする。一般に、推力$F$ は、$V$の二乗に比例すると考えられているので、次の式を考える。

$$\begin{equation}F=\delta V^{2}\end{equation}\label{eq3}$$

ここで、$\delta$は、ある与えられたプロペラの元でのモーターパワーを表すパラメータと考えれば良い。

PID制御のP制御（比例制御）を次の式で導入する。微分（D）制御も入れることは可能だが、以下計算がさらに複雑になるので、次の課題とする。ただし、D制御を入れないと安定化しない場合があるので、それは念頭に置いておかなければならない。（D制御を入れたモデルは、次の記事で行なっているPID制御によるドローンの揺れに関する数値シミュレーション（４）：P制御＋D制御モデル）

$$\begin{equation}V=V_{0}-p\theta\end{equation}\label{eq4}$$

ここで、$V_{0}$は、ホバリングを実現可能なスロットルレベルに対応したモーターの回転数である。$p$は、P制御の水準である。すなわち、このシミュレーションモデルにある唯一の制御変数である。$\theta$はピッチ角なので、ピッチ角に比例してモーターの回転数を制御することになる。ピッチ角がゼロの時は、ホバリングレベルのモーター回転数で、ピッチが正になると回転数を落とす方向に、逆に負になると回転数を増やす方向に変化させる。

私が自作のドローンで問題視しているのは、この制御信号が回転数に変化する上で200m秒くらいタイムラグがあることだ。それを本来調べるためのこの数値シミュレーションをしようと思ったのだが、そのタイムラグを入れるのは次の課題としてて、まず、タイムラグなしにESC信号をモータは回転数に反映させるとここでは考えている。（制御の遅延を組み込んだモデルは、このシリーズの「（６）の記事」以降で解析している）

この制御式$\eqref{eq4}$を、回転数と力の関係$\eqref{eq3}$に入れる。

$$\begin{equation}F=\delta V^{2}=\delta (V_{0}-p\theta)^{2}=\delta V_{0}^{2}-2p\delta V_{0}\theta+p^{2}\delta \theta^{2}\end{equation}\label{eq5}$$

簡単化かのためにこの式を次のように表そう。

$$\begin{equation}F=\alpha-\beta\theta+\gamma\theta^{2}\end{equation}\label{eq6}$$

ここで、$\alpha, \beta, \gamma$の各パラメータは、$\eqref{eq5}$式の各パラメータを表している。この式を運動方程式$\eqref{eq5}$に代入すると、次の式を得る。

$$\begin{equation}mL\frac{d^{2}\theta}{dt^{2}}=\alpha-mg\cos \theta-\beta \theta+\gamma \theta^{2} \end{equation}\label{eq7}$$

両辺を$mL$で割ると、

$$\begin{equation}\frac{d^{2}\theta}{dt^{2}}=\frac{1}{L}\left(\frac{\alpha}{m}-g\cos \theta\right)-\frac{\beta \theta}{mL}+\frac{\gamma}{mL} \theta^{2} \end{equation}\label{eq8}$$

を得る。これは、二階非線型常微分方程式である。これを満たす$\theta$の振る舞いについて、解析的を求める方法が有るかどうかはわからなかった。しかし、ここでおこなう数値シミュレーションはこのままの形で実行可能、実際、あとでその結果を示すことができる。

ただ、その前に、ここでは議論をわかりやすくするために、$\theta$の値が小さい範囲で成立する、

$$\cos\theta\simeq 1$$

という近似を用いて議論の見通しをよくする。この時、$\eqref{eq8}$は、次のように書き換えることができる。

$$\begin{equation}\frac{d^{2}\theta}{dt^{2}}=\frac{1}{L}\left(\frac{\alpha}{m}-g\right)-\frac{\beta \theta}{mL}+\frac{\gamma}{mL} \theta^{2} \end{equation}\label{eq9}$$

これもまた、二階非線型常微分方程式であるが、これには解析解が存在している。（例えば. http://www6338.la.coocan.jp/mathematics/diff-equation.pdf 参照）しかし、それはワイエルシュトラスの$\wp$関数を用いて表現される楕円関数を使うもので、そこまで複雑なものは上手く扱えない。

そこで、さらに、この$\theta$の二乗の項（右辺最後の項）が存在しなかった場合を考えてみよう。すなわち、

$$\begin{equation}\frac{d^{2}\theta}{dt^{2}}=\frac{1}{L}\left(\frac{\alpha}{m}-g\right)-\frac{\beta \theta}{mL}\end{equation}\label{eq10}$$

となる。これは、高校物理でもお馴染みの、中心が原点以外のところにある単振動の式に他ならない。詳しくは教科書を見ていただきたいが、これは、周期$T$が、

$$T=2\pi\sqrt{\frac{mL}{2pV_{0}\delta}}$$

単振動の中心位置 $\theta_{0}$が、

$$\theta_{0}=\frac{1}{2p}\left(V_{0}-\frac{mg}{V_{0}\delta}\right)$$

となるものである。つまり、振動への傾向は、このモデルに内蔵されているということである。しかし、制御機能があるので、その振動は安定、すなわち一定の時間が経てば収束する可能性ももちろん持っている。

また、$\theta$が小さい範囲ということは、また、最終項の$\theta^{2}$も小さいと考えることもできるので、そうなると、このリアリティは重要だ。しかし、実際のドローンは、わずかな傾きでも、水平方向へ移動する。水平移動は、まだモデルに組み込んでいないので、このシミュレーションには現れない（いずれ組み込みたい）。このような振動の影響の大きさを考えると、この近似は避けるべきだ。

そこで、ここでは$\eqref{eq8}$そのものの数値シミュレーションを行うことにする。ここからは、次の記事（２）で解説する。

このシリーズの記事の目次は次のところにある。

目次：PID制御によるドローンの揺れに関する数値シミュレーション