前の（９）では、遅延制御による問題を回避するためにジャイロ効果を利用する理論的モデルを示した。ここでは二階の非線型常微分方程式と数値解用の漸化式で表されたモデルを、計算で解いた結果を示す。
これまでの記事は以下のリンクから見ることができる。
シミュレーションで使用したc++のプログラムは、次のgithubのレポジトリから取得できる。gyroeffect-1.cppという名前のファイルである。
https://github.com/toyowa/pidsimulation/tree/main
シミュレーション結果を示す。まず、試行錯誤の末に到達した最もよい結果から示す。制御の遅延レベルは、実機の実態を反映した200msに統一している。
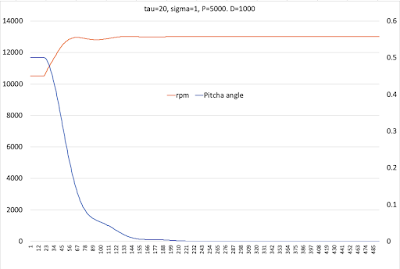
１。遅延20期（200ms）、σ = 1.0、P=5000. D=1000
青い線が、機体のピッチ角である。オレンジの線は、モータの回転rpmである。ほぼ迷いなくホバリングの水平姿勢に向け一直線に姿勢を正している。腕の長さや重量などを実機のままに、遅延20期は、これまで全て飛行破綻状態だったが、初めて、遅延のない制御とほぼ同じ結果がもたらされた。おろどくべきことだ。
２。遅延20期（200ms）、σ = 0.5、P=5000. D=1000
他は同じで、ジャイロ効果を半分まで小さくすると、初期の揺れののちにホバリング姿勢に収束していく。
これよりも小さく、例えばシグマを0.25とすると、飛行はすぐに破綻する。すなわち、ジャイロ効果のない事態に近づいていくのである。
逆にシグマを増加させてみよう。
３。遅延20期（200ms）、σ = 2.0、P=5000. D=1000
PIDのスケールを変えたものも行ったが、ここでのPDの値で、シグマが1.0あたりが一番、綺麗に制御されているように思う。
いずれにしても、ジャイロ効果は、PIDの制御遅延の問題を解決する上で、大きな効果と意味があることがわかった。
0 件のコメント:
コメントを投稿