PID制御によるドローンの揺れに関する数値シミュレーション（１１）：ジャイロモーメント

 前節で、制御遅延があるシステムに、機体の慣性モーメントを増やすために、ジャイロ効果を入れた時のシミュレーションを行なった。運動方程式上は、角速度に係数$\sigma$をかけたものが入ってきた。そして、その$\sigma$はある程度の大きさを持っていないと、PID制御による安定化に寄与できないことがわかった。そこで、一体どうしたらこのようなジャイロ効果を入れることができるのかを考えてみる。

なにしろ、ドローンは中空を飛んでいるのである。慣性モーメントを増やそうというのは、特に支えもないのに動きにくくしようということである。

プロペラにもジャイロ効果があると書いた。それは大概対称に回転しているので、ジャイロ効果も偏りなく入ってきそうであるが、残念ながらその効果は大きくない。なぜなら、プロペラが軽いからである。

そこで、フライホイールのように円板を回転させて、それによって生み出されるジャイロ効果を組み込むことを考えよう。回転体は、コマのように一つの方向を維持しようとし、力を加えると歳差運動を引き起こす。

回転体に、その軸と垂直にひねりの力を加えると、それに対する反発力としてのジャイロモーメントが生まれる。この力は、結局ひねりそのものを抑止する力となる。

この仮説が正しいとして、それによって我々の$\sigma$の値を得るためには、どれほどの回転体を用意しなければならないかを数値分析しようというのが、ここでの課題である。

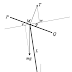
まず、フライホイールの図を用意する。

中央の網掛け部分がフライホイールの本体、回転体である。

まず、この円板の慣性モーメント$I$を求めると次のようになる。それほど難しくないと思うが、Wikipediaのものをそのまま使っている。円板は、質量$M$が均等に分布し、半径$a$のものである。

$$I=\frac{1}{2}a^{2}M$$

この慣性モーメントはベクトルではなくスカラー値である。一方、この回転から生じている円板の角運動量は円板の角速度$\vec{\omega}$と慣性モーメントによって次のように表される。（ベクトルの矢印が少しずれています）

$$\vec{U}=I\vec{\omega}$$

今、回転体が上側にいる観察者から見て、反時計回りに回転していると、右ネジ方向がベクトルの向きになる。従って、角運動量ベクトル同じ上方向になる。

一方、ジャイロモーメント$\vec{T_{g}}$は、軸をひねる角速度を$\vec{\Omega}$として、次のようになる。Wikipedi

$$\vec{T_{g}}=\vec{U}\times\vec{\Omega}$$

ここでは、ひねりは軸に対して垂直に加えられるとする。$\times$はベクトルの外積であり、それ自身ベクトルだが、今はスカラー値を観察する。両ベクトルが垂直の関係なので、ベクトルを外した記号の式で、目的のものが求められる。

今、回転体の中心から捻りを与えるまでの距離を$L$とする。これは、ドローン機体の中心からモータの位置までを想定すればよい。モータこそがフライホイールに捻りを与える存在だからである。実際は、回転体は、機体に水平に置かれるが、それは大きな問題ではない。

スカラー値だけを問題にして、まず、$\Omega=\frac{d\theta}{dt}$だから、

$$U=I\omega$$

$$T_{g}=U\frac{d\theta}{dt}$$

また、$T_{g}$は、トルクであるから、その力を$F$として、

$$T_{g}=LF=U\frac{d\theta}{dt}=\frac{1}{2}a^{2}M\omega\frac{d\theta}{dt}$$

$$F=\frac{a^{2}M\omega}{2L}\frac{d\theta}{dt}$$

と書き換えられる。

また、円板の毎分回転数$R$(rpm)は、円板の回転の角速度$\omega$を使って、次のように求められる。

$$R=\frac{\omega}{2\pi}60=\frac{30\omega}{\pi}$$

逆に$\omega$で解いて、

$$\omega=\frac{\pi R}{30}$$

を得る。

これで、準備が整ったはずだ。

以上の変形を使うと、このシリーズの（９）に記載されている遅延制御とジャイロ効果を含む運動式の、ジャイロ効果の項（マイナスを省く）は次のようになる。

$$\sigma\frac{d\theta}{dt}=\frac{F}{mL}=\frac{a^{2}M\frac{\pi R}{30}}{2L}\frac{d\theta}{dt}$$

左端と右端の項を比べることによって次の式を得る。

$$\sigma=\frac{\pi a_{2}MR}{60L}$$

この式の右辺に、実際の円板と実機の情報を次のように与える。

$$M=0.113 (Kg)$$

$$a=0.1 (m)$$

$$R=5000 (rpm)$$

$$L=0.215 (m)$$

円板は、厚さ１.5mm、半径100mmステンレス板であり重さは大体113グラムくらいになる。比較的小さなブラシレスモーター（負荷は小さいのでKv値が大きくてよい）で回す予定で、5000rpmを想定する。また、ドローンの腕の長さは、これまで通り21.5cmである。

これらの値を上式に代入すると、計算間違いがなければ、$\sigma$は次のようになる。

$$\sigma \simeq 1.3753 $$

（１０）のシミュレーションで、$\sigma$は1以上であれば、PID制御によって一方的安定化が可能であることが示されている。従って、ここで想定するフライホイールでそれが可能になることが示されたわけだ。

もし、不足したり、過大であったりするときは円板の回転数を上下させればよい。あるいは、急な旋回や機体の移動が必要なときは、このジャイロモーメントは邪魔になるので、回転を止めることも必要になるだろう。

ただし、機体を抑止する方向は、一つの円板で一つの方向しかダメなので、水平方向の揺れを抑止するためには、少なくとも二つの円盤を動かさなければならないことに注意する。

これまでの記事は以下にある。

目次：PID制御によるドローンの揺れに関する数値シミュレーション