複数プロペラドローンの機体の安定は、PID制御などによってプロペラ相互の回転速度を変化させることで実現してきた。ここでは、回転速度は一定のまま、プロペラの回転面の方向を変えることによって実現できないかを少し考えてみたい。
とは言っても、ヘリコプターは、実質回転面を変化させているので、すでになじみの方法なのかもしれない。そこで、まず、プロペラが一個にして状況を単純化しこのことを考えてみたい。
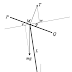
次の図を見ていただきたい。
ここで、OMは、長さLの質量を無視できる房であるとしよう。ドローンの機体を抽象化したものだ。機体は、位置が固定しているO点を支点として回転するのみである。Mにモーターとプロペラがありがあり、プロペラの回転面はMを支点に自由に動かすことができるとして、その回転面は直線PQで表されている。プロペラの回転面は、機体に対して垂直な状態が基準である。機体OMは垂直に立っている状態が基準となる。そこからの機体の傾きを図の$\theta$ で表される。また、機体のプロペラ面の基準状態からの傾きは、$\varphi$で表されている。
機体の質量は点Mに全て代表して存在し$m$で表される。重力加速度をgとしよう。M点の運動方程式を考える。プロペラの回転数は一定で、そのスロットルは一定の力$T$で表されるとしよう。
また、二つの角度$\varphi$と$\theta$は図の方向が正の方向であるとする。
$mL\frac{d^{2}\theta}{dt^{2}}=mg\sin\theta-T\sin\varphi$
となる。今、プロペラ面の角度を制御するスキームとして、次の式を考える。
$\varphi=\delta\theta$
つまり、機体の傾き角度に応じて一定の係数$\delta$をかけてプロペラ面を制御するというものである。このとき、運動方程式にこの式を代入し変形すると、次のようになる。
$\frac{d^{2}\theta}{dt^{2}}=-(\frac{T}{mL}\sin\delta\theta-\frac{g}{L}\sin\theta)$
$\frac{d^{2}\theta}{dt^{2}}=-(\frac{T}{mL}\sin(\delta\theta+\eta\frac{d\theta}{dt})-\frac{g}{L}\sin\theta)$
右辺のカッコ内の第1項を三角関数の加法定理を使って変形すると次のようになる。
$\frac{d^{2}\theta}{dt^{2}}=-(\frac{T}{mL}(\sin(\delta\theta)\cos(\eta\frac{d\theta}{dt})+\cos(\delta\theta)\sin(\eta\frac{d\theta}{dt}))-\frac{g}{L}\sin\theta)$
今、$\theta$が微小な範囲でのみ変化するとして、$\sin\beta\sim\beta, \cos\beta\sim 1$という近似を持ちいると、
$\frac{d^{2}\theta}{dt^{2}}=-(\frac{T}{mL}(\delta\theta+\eta\frac{d\theta}{dt})-\frac{g}{L}\theta)$
単振動にはならないので、二階同次微分方程式の形にしておこう。
$\frac{d^{2}\theta}{dt^{2}}+\frac{\eta T}{mL}\frac{d\theta}{dt}+(\frac{\delta T}{mL}-\frac{g}{L})\theta=0$