以下のリストにある以前のシミュレーションは、ドローンをローターの位置のみを質点としてみたシミュレーションだった。
目次:PID制御によるドローンの揺れに関する数値シミュレーション
すなわち、4ロータードローンならば、機体重が4つのローター位置に分散している4質点を想定したものだった。それでも、PID制御の特質を捉えることはできると思っているが、実体的には、ドローンを連続的な質点が分布している剛体として分析すべきだろう。
そこで、引き続き、極力、単純性を確保しながら剛体としてのPID制御によるドローン姿勢制御のシミュレーションを試みることにした。
空間を自由に姿勢を変えながら動くドローンの運動は、オイラーの運動方程式を使うかラグランジュの方程式を使うかという選択があるが、ここではオイラーの運動方程式を、一軸固定で簡単化して使うことにする。
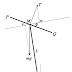
そこで、ローターを前から右回りに1、2、3、4と番号をつけ、1番画のロータが最前方にあるとし、1と3のローターを貫く方向を軸とした回転をロールとして、2、4を軸とする回転をピッチとしよう。そして、ロールの回転だけ分析することにする。
ここで、ドローンのロール方向の慣性モーメントを$I$としよう。慣性モーメントは回転のしにくさ、あるいは回転のおもたさのようなものであり、ドローンの部品の重さと位置を悉く把握できれば、近似的に計算できなくもないが、なかなか面倒なものである。現実の物体の動きから逆算的に慣性モーメントを推定したりすることもあるようだ。ここでは何らかの方法で計算されているとしよう。
このように慣性モーメントが出てくるところが、剛体としてのドローンを捉える最も重要なステップであると言える。
二つのローターによる推力は、$f_{1}$と$f_{2}$によって与えられる。前後の軸、ここでは$x$方向の軸は固定されているとする。したがって、この固定された軸の回転のみを解析することになる。したがって上下方向の動きは想定していない。PID制御による揺らぎからの安定性のみを分析するということである。
左回りを正の方向とした機体角度を$\theta$で表す(モータの一関係上、ロール角の方向は負となるが特に問題ではない)。その正の方向に回転する角速度を$\omega$とする。したがって角速度ベクトルは画面手前側($x$軸の正方向)に向いていることになる。ただ、この方向はあまり関係はない。機体の中心を原点$O$として、ここからローターまでの長さを$L$で表す。
この1軸固定の剛体の運動方程式は次のように表される。
$$I\frac{d\omega}{dt}=L(f_{1}-f_{2})$$
オイラーの運動方程式で、一つの回転方向しか見ない特殊な場合でもある。この辺りのわかりやすい理論的説明は原島鮮氏の『力学I 質点・剛体の力学(新装版)』(p.193)に与えられている。
運動方程式の右辺は、二つのローターによるトルクの差を表している。このトルク差が回転の動力を与えるのである。
プロペラの回転による$f_{1}$および$f_{2}$の変化は、次の各式で与えられると想定する。設定は、前のシミュレーションモデルと同じであり、必要ならば参照していただきたい。
$$f_{1}=\delta\left(V_{0}-P\theta-D\frac{d\theta}{dt}\right)^{2}$$
$$f_{2}=\delta\left(V_{0}+P\theta+D\frac{d\theta}{dt}\right)^{2}$$
$V_{0}$は、ホバリングを実現するプロペラの回転数で1軸固定を正当化する力である。$P$は、PID制御のPパラメータで、単位としては機体のロール角(ラディアン)をプロペラ回転数に変換するものである。また、$D$は、PIDの微分制御で、ロールの角速度をプロペラ回転数に変換するパラメータである。ここでは、機体の傾向的偏差を補正する $I$制御は考慮しない。
プロペラの回転数は、その平方値が力に比例すると考える。また、その変換パラメータが$\delta$になっている。
このトルクに関する二つの式を運動方程式に代入して整理すると次の式を得る。
$$I\frac{d\omega}{dt}=-4L\delta V_{0}\left(P\theta+D\frac{d\theta}{dt}\right)$$
さらに、$w=\frac{d\theta}{dt}$を用いて整理すると次のようになる。
$$\frac{d^{2}\theta}{dt^{2}}+4\frac{L\delta V_{0}D}{I}\frac{d\theta}{dt}+4\frac{L\delta V_{0}P}{I}=0$$
ここで、
$$4\frac{L\delta V_{0}}{I}=\eta$$とおく。この$\eta$は時間に依存しない定数である。すると式は、
$$\frac{d^{2}\theta}{dt^{2}}+\eta D\frac{d\theta}{dt}+\eta P=0$$
となり、典型的な二階の線形常微分方程式となった。もっと複雑になるかと思ったが、予想外に単純なモデルとなったことにとても驚いた。
これは微分方程式の教科書にも必ず書いてあるもので、解析的に解くことも容易である。
特性方程式は次のようになる。
$$\lambda^{2}+\eta D\lambda+\eta P=0$$
この式の判別式を$J$とすると、
$$J=\eta^{2}D^{2}-4\eta P = D^{2}\eta\left(\eta-\frac{4P}{D^{2}}\right)$$
三つの場合に分けることができる。
(1)$0<\eta<\frac{4P}{D^{2}}$のとき、$J<0$で、特性式を満たす$\lambda$は、虚数になる。
$$\lambda = \frac{-\eta D\pm \sqrt{\eta^{2}D^{2}-4\eta P }}{2}=\alpha\pm\beta I$$
とすると、解である$\theta$は、次のようになる。
$$\theta=e^{\alpha t}(C_{1}\cos{\beta t}+C_{2}\sin{\beta t})$$
ここで、$C_{1}, C_{2}$は、初期条件から与えられる未定条数で、これで初期の撹乱を与えることができる。。
$\alpha=-\frac{\eta D}{2} < 0$であるから、この場合は、機体角度は振動しながら減衰し、ホバリング状態に近づいていく。
(2)$J=0$で、重根のとき。
$\lambda=\alpha=\frac{-\eta D}{2}$として、
$$\theta=e^{\alpha t}(C_{1}+C_{2}t)$$
で、機体角度は、揺れることもなく、ホバリング状態に減衰していく。
(3)$J>0$で、実数解のとき。特性方程式の解を$\lambda_{1}, \lambda_{2}$とすると、
$$\theta=C_{1}e^{\lambda_{1}t}+C_{2}e^{\lambda_{2}t}$$
となる。特性方程式は二次曲線だが、その中心は負にあり、かつ$\lambda=0$の左辺の値は、正なので、この二つの解は、必ず負である。したがって、この場合もまた一方的に機体角度はホバリング状態に近づいていく。
機体に撹乱があったとき、どのような状況でも、時間の速さや揺れがある内の違いはあっても、ホバリング状態に戻ることがわかった。また、$\eta$の絶対値が大きくなると、ホバリング状態への復帰が早くなる。$\eta$の定義から、他が同じで、慣性モーメントが大きくなるとホバリング状態への復帰が遅くなることを意味している。期待が大きくなると必然的に慣性モーメントは大きくなるので、安定化に時間がかかるということだ。ある意味当然の結果だと言える。
他のパラメータの影響も色々調べることはできるが、それはまた機体の設計上、必要に応じてやるのが効率的なので、ここではこれ以上の分析はスキップする。
確認のために、数値的なシミュレーションを実行しよう。ただし、解析的にある程度解がわかっているので、パラメータを実機に近いものにする面倒は避けておく。
(1)虚数解のとき
パラメータを条件に合わせて次のようにする。$c_{1}=2, c_{2}= 1, \eta=0.0015, D=2, P=1$このときステップを1秒として実行すると解の機体角度$\theta$は次のようになる。
理論的に予測された通りである。
重根のときは省略。
(2)実数解のとき
パラメータは、虚数解と比べて$P=0.001$だけを変更する。P制御を弱めた形になる。結果は次のようだ。
一方的減数で、予想どおりだ。
これらの結果は、PID制御が有効なことを表しているが、問題は、制御に遅延がある場合、すなわちむだ時間がある場合である。先のシミュレーションでは、むだ時間がある場合は、安定化はとても難しかった。
また、むだ時間を入れる場合は、解析的な解は望めない。その辺りを次に検討するつもりだ。